[r] Read Three Columns and Make a Matrix From It

Matrix is a rectangular arrangement of numbers in rows and columns. In a matrix, as nosotros know rows are the ones that run horizontally and columns are the ones that run vertically. In R programming, matrices are two-dimensional, homogeneous data structures. These are some examples of matrices:

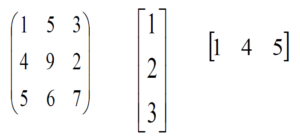
Creating a Matrix

To create a matrix in R you need to use the function called matrix(). The arguments to this matrix() are the prepare of elements in the vector. Y'all have to laissez passer how many numbers of rows and how many numbers of columns you want to have in your matrix.

Notation: By default, matrices are in cavalcade-wise order.

Python3

A = matrix(

c( 1 , 2 , 3 , iv , v , half-dozen , 7 , 8 , 9 ),

nrow = three ,

ncol = iii ,

byrow = True

)

rownames(A) = c( "a" , "b" , "c" )

colnames(A) = c( "c" , "d" , "east" )

true cat( "The 3x3 matrix:\northward" )

print (A)

Output:

The 3x3 matrix:   c d eastward a 1 2 3 b 4 5 6 c 7 8 9

Creating special matrices

R allows cosmos of various different types of matrices with the use of arguments passed to the matrix() function.

• Matrix where all rows and columns are filled past a single constant 'k':
  To create such a matrix the syntax is given below:
  

Syntax: matrix(k, m, n)
Parameters:
k: the constant
m: no of rows
n: no of columns

• Example:
  

Python3

• Output:
  

          [,1] [,2] [,3] [1,]    5    5    five [2,]    v    v    5 [three,]    5    v    5

• Diagonal matrix:
  A diagonal matrix is a matrix in which the entries outside the chief diagonal are all zero. To create such a matrix the syntax is given below:
  

Syntax: diag(k, m, n)
Parameters:
k: the constants/array
m: no of rows
due north: no of columns

• Case:
  

Python3

print (diag(c( 5 , 3 , iii ), three , 3 ))

• Output:
  

          [,one] [,ii] [,iii] [1,]    v    0    0 [2,]    0    three    0 [3,]    0    0    iii

• Identity matrix:
  A square matrix in which all the elements of the principal diagonal are ones and all other elements are zeros. To create such a matrix the syntax is given below:
  

Syntax: diag(k, m, n)
Parameters:
k: i
m: no of rows
n: no of columns

• Case:
  

Python3

• Output:
  

          [,1] [,2] [,3] [one,]    1    0    0 [two,]    0    i    0 [3,]    0    0    one

Matrix metrics

Matrix metrics mean once a matrix is created then

• How can you know the dimension of the matrix?
• How can you lot know how many rows are there in the matrix?
• How many columns are in the matrix?
• How many elements are there in the matrix? are the questions we generally wanted to answer.

Example:

Python3

A = matrix(

c( 1 , two , 3 , iv , five , 6 , 7 , 8 , ix ),

nrow = 3 ,

ncol = 3 ,

byrow = TRUE

)

cat( "The 3x3 matrix:\n" )

print (A)

cat( "Dimension of the matrix:\n" )

print (dim(A))

cat( "Number of rows:\northward" )

impress (nrow(A))

cat( "Number of columns:\north" )

impress (ncol(A))

cat( "Number of elements:\n" )

print (length(A))

print (prod(dim(A)))

Output:

The 3x3 matrix:      [,ane] [,two] [,iii] [ane,]    1    2    three [2,]    4    v    6 [3,]    seven    eight    nine Dimension of the matrix: [i] iii three Number of rows: [one] three Number of columns: [1] 3 Number of elements: [i] 9 [1] 9

Accessing elements of a Matrix

Nosotros tin access elements in the matrices using the same convention that is followed in data frames. Then, you volition accept a matrix and followed by a foursquare bracket with a comma in between array. Value earlier the comma is used to access rows and value that is after the comma is used to admission columns. Let's illustrate this by taking a elementary R code.
Accessing rows:

Python3

A = matrix(

c( 1 , 2 , 3 , iv , 5 , 6 , seven , 8 , 9 ),

nrow = 3 ,

ncol = iii ,

byrow = TRUE

)

true cat( "The 3x3 matrix:\n" )

impress (A)

cat( "Accessing showtime and 2d row\n" )

print (A[ i : two , ])

Output:

The 3x3 matrix:      [, 1] [, 2] [, three] [ane, ]    1    2    3 [2, ]    4    five    6 [3, ]    seven    8    ix  Accessing first and second row      [, one] [, 2] [, 3] [one, ]    i    2    3 [2, ]    4    five    6

Accessing columns:

Python3

A = matrix(

c( 1 , 2 , 3 , iv , five , 6 , 7 , viii , 9 ),

nrow = iii ,

ncol = 3 ,

byrow = Truthful

)

true cat( "The 3x3 matrix:\n" )

print (A)

cat( "Accessing start and second column\n" )

print (A[, ane : 2 ])

Output:

The 3x3 matrix:      [, 1] [, two] [, 3] [1, ]    1    2    3 [2, ]    4    five    6 [3, ]    7    eight    9  Accessing starting time and second column      [, 1] [, two] [1, ]    one    two [ii, ]    4    v [3, ]    7    8

Accessing elements of a matrix:

Python3

A = matrix(

c( 1 , 2 , iii , 4 , 5 , 6 , 7 , 8 , 9 ),

nrow = iii ,

ncol = three ,

byrow = TRUE

)

cat( "The 3x3 matrix:\n" )

print (A)

impress (A[ 1 , 2 ])

impress (A[ 2 , 3 ])

Output:

The 3x3 matrix:      [, i] [, two] [, three] [ane, ]    1    2    3 [ii, ]    4    5    half dozen [3, ]    seven    eight    9  [one] 2 [1] vi

Accessing Submatrices:
We can admission submatrix in a matrix using the colon(:) operator.

Python3

A = matrix(

c( 1 , 2 , 3 , 4 , 5 , six , vii , 8 , 9 ),

nrow = three ,

ncol = three ,

byrow = TRUE

)

true cat( "The 3x3 matrix:\n" )

impress (A)

cat( "Accessing the kickoff three rows and the first two columns\n" )

print (A[ 1 : 3 , ane : ii ])

Output:

The 3x3 matrix:      [, 1] [, 2] [, 3] [1, ]    1    2    three [ii, ]    four    5    half-dozen [3, ]    7    eight    9  Accessing the first three rows and the first two columns      [, i] [, ii] [one, ]    1    two [2, ]    iv    5 [3, ]    7    viii

Modifying elements of a Matrix

In R y'all tin can modify the elements of the matrices by a direct assignment.
Case:

Python3

A = matrix(

c( i , 2 , three , four , 5 , 6 , 7 , 8 , 9 ),

nrow = 3 ,

ncol = iii ,

byrow = True

)

cat( "The 3x3 matrix:\due north" )

print (A)

A[ three , three ] = 30

cat( "After edited the matrix\due north" )

print (A)

Output:

The 3x3 matrix:      [, 1] [, 2] [, iii] [1, ]    1    2    three [2, ]    4    5    6 [3, ]    7    eight    9  Later on edited the matrix      [, ane] [, 2] [, 3] [ane, ]    1    2    three [ii, ]    4    5    6 [three, ]    seven    8   30

Matrix Concatenation

Matrix chain refers to the merging of rows or columns of an existing matrix.
Concatenation of a row:
The concatenation of a row to a matrix is done using rbind().

Python3

A = matrix(

c( i , ii , 3 , iv , 5 , 6 , 7 , viii , ix ),

nrow = 3 ,

ncol = iii ,

byrow = True

)

true cat( "The 3x3 matrix:\n" )

print (A)

B = matrix(

c( 10 , 11 , 12 ),

nrow = one ,

ncol = 3

)

cat( "The 1x3 matrix:\n" )

impress (B)

C = rbind(A, B)

cat( "Afterwards concatenation of a row:\northward" )

print (C)

Output:

The 3x3 matrix:      [, 1] [, ii] [, iii] [ane, ]    1    2    3 [2, ]    4    5    6 [iii, ]    vii    eight    9  The 1x3 matrix:      [, 1] [, ii] [, 3] [1, ]   ten   11   12  Afterwards chain of a row:      [, 1] [, two] [, 3] [1, ]    ane    2    3 [2, ]    4    5    six [3, ]    7    8    9 [4, ]   10   eleven   12

Concatenation of a column:
The concatenation of a cavalcade to a matrix is done using cbind().

Python3

A = matrix(

c( ane , 2 , 3 , 4 , 5 , half-dozen , vii , 8 , ix ),

nrow = 3 ,

ncol = 3 ,

byrow = TRUE

)

cat( "The 3x3 matrix:\northward" )

impress (A)

B = matrix(

c( 10 , 11 , 12 ),

nrow = three ,

ncol = i ,

byrow = TRUE

)

cat( "The 3x1 matrix:\n" )

print (B)

C = cbind(A, B)

cat( "After concatenation of a cavalcade:\northward" )

print (C)

Output:

The 3x3 matrix:      [, 1] [, 2] [, iii] [i, ]    1    2    iii [two, ]    four    five    vi [3, ]    7    8    9  The 3x1 matrix:      [, 1] [1, ]   10 [2, ]   11 [3, ]   12  Afterwards chain of a cavalcade:      [, i] [, ii] [, 3] [, 4] [i, ]    ane    2    3   10 [2, ]    4    5    6   11 [3, ]    7    8    9   12

Dimension inconsistency: Note that you have to make sure the consistency of dimensions between the matrix earlier yous exercise this matrix chain.

Python3

A = matrix(

c( one , 2 , iii , 4 , five , half dozen , 7 , eight , 9 ),

nrow = iii ,

ncol = 3 ,

byrow = True

)

cat( "The 3x3 matrix:\n" )

impress (A)

B = matrix(

c( 10 , 11 , 12 ),

nrow = 1 ,

ncol = 3 ,

)

cat( "The 1x3 matrix:\due north" )

print (B)

C = cbind(A, B)

true cat( "After chain of a column:\n" )

print (C)

Output:

The 3x3 matrix:      [, 1] [, ii] [, 3] [one, ]    1    2    3 [two, ]    iv    v    6 [iii, ]    7    8    9  The 1x3 matrix:      [, ane] [, ii] [, 3] [1, ]   10   11   12  Error in cbind(A, B) : number of rows of matrices must match (meet arg 2)

Deleting rows and columns of a Matrix

To delete a row or a column, beginning of all, you demand to access that row or column and and then insert a negative sign earlier that row or column. Information technology indicates that you had to delete that row or column.
Row deletion:

Python3

A = matrix(

c( ane , ii , 3 , iv , 5 , 6 , seven , eight , 9 ),

nrow = iii ,

ncol = 3 ,

byrow = TRUE

)

cat( "Before deleting the second row\northward" )

print (A)

A = A[ - 2 , ]

cat( "Later on deleted the 2nd row\n" )

impress (A)

Output:

Before deleting the 2nd row      [, 1] [, ii] [, iii] [1, ]    1    ii    iii [2, ]    4    5    6 [3, ]    seven    eight    ix  After deleted the 2nd row      [, 1] [, 2] [, 3] [i, ]    1    2    three [2, ]    7    8    9

Cavalcade deletion:

Python3

A = matrix(

c( i , 2 , 3 , iv , 5 , six , 7 , eight , nine ),

nrow = 3 ,

ncol = 3 ,

byrow = TRUE

)

true cat( "Before deleting the second column\n" )

print (A)

A = A[, - ii ]

cat( "Afterward deleted the 2nd column\n" )

print (A)

Output:

Before deleting the 2nd column      [, 1] [, 2] [, 3] [1, ]    1    2    iii [2, ]    iv    5    6 [3, ]    7    8    9  Later deleted the 2d column      [, 1] [, 2] [1, ]    1    iii [2, ]    4    6 [iii, ]    7    9

earnestdecong.blogspot.com

Source: https://www.geeksforgeeks.org/r-matrices/

Share this post